Взаимосвязи между целевыми показателями прибыли и рентабельности
Дитгер Хан 'ПиК: Планирование и контроль: концепция контроллинга'
II. Характеристика интегрированных ориентированных на результат и ликвидность планово-контрольных расчетов
3. Связи между целевыми показателями результата, рентабельности и ликвидности
3.1. Взаимосвязи между целевыми показателями прибыли и рентабельности
3.1.1. Взаимосвязи при постоянном и переменном капитале
Прежде всего интерес представляет соотношение целей максимизации прибыли и максимизации рентабельности капитала и особенно вопрос, достигаются ли обе эти цели при одном и том же объеме производства или при различных объемах производства. В последнем случае эти цели оказывают различное влияние на предпринимательские решения об объемах производства продукции.
Если определить эти цели сначала недифференцированно в виде
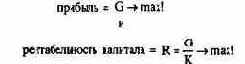
то очевидно, что при условии постоянства капитала (К) выбор в качестве целевых показателей прибыли и рентабельности не может оказывать различного влияния на предпринимательские решения, поскольку при постоянном значении знаменателя (К) рентабельность (R) будет максимальна в случае максимизации числителя (G). Обе цели - максимизация прибыли и рентабельности - в этом случае дополняющие одна другую. При дифференцировании капитала на постоянную и переменную составляющие получается:
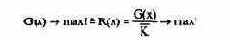
При этом условии максимизация рентабельности капитала достигается путем максимизации прибыли, т.е. максимум рентабельности капитала достигается при таком же объеме производства х, при котором достигается максимальная прибыль. Это происходит в случае нелинейной функции при равенстве предельных издержек и предельной выручки:
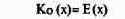
Если исходить в краткосрочном и среднесрочном периодах из постоянства (неизменности) капитала, то через формулу рентабельности инвестированного капитала (RoI) графическим путем можно наглядно показать взаимосвязи между рентабельностью капитала, рентабельностью оборота и скоростью оборота капитала. На рис. 27 видно, что рентабельность оборота и оборачиваемость капитала являются ключевыми переменными, определяющими величину рентабельности капитала.
Дитгер Хан 'ПиК: Планирование и контроль: концепция контроллинга'
II. Характеристика интегрированных ориентированных на результат и ликвидность планово-контрольных расчетов
3. Связи между целевыми показателями результата, рентабельности и ликвидности
3.2. Взаимосвязи между целевыми показателями прибыли и оборота
Взаимосвязи между целями максимизации прибыли и оборота существенно проще для понимания. Стремление к максимизации оборота рассматривается здесь как важнейшее выражение стремления к росту. Показатель оборота - один из компонентов, расчета показателя прибыли. Из функции G(х) = Е(х) - Ко(х) можно вывести соответствующие взаимосвязи между целями. При нереальном условии постоянства издержек (Ко) целевые показатели становятся взаимодополняющими, т.е. постановка различных целей приводит к одинаковым предпринимательским решениям.
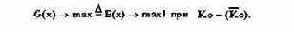
Если отказаться от нереального условия неизменности издержек, то взаимосвязи между целями максимизации прибыли и максимизации оборота (выручки) необходимо анализировать, беря за основу соответствующие кривые издержек и выручки.
В самом простом случае функции издержек и выручки линейны. Из рис. 30 видно, что цели максимизации прибыли и оборота полностью взаимодополняемы. Максимальные значения обеих функций лежат в области бесконечности или определяются пределом производственной мощности. В первом случае на рис. 29 при линейной функции издержек и функции выручки, соответствующей предполагаемой функции цена - сбыт, легко увидеть, что на отдельных участках взаимосвязи между целями частично непостоянны. Во втором случае на рис. 29 при дегрессивно-прогрессивной функции издержек и линейной функции выручки взаимосвязи между целями также частично непостоянны.
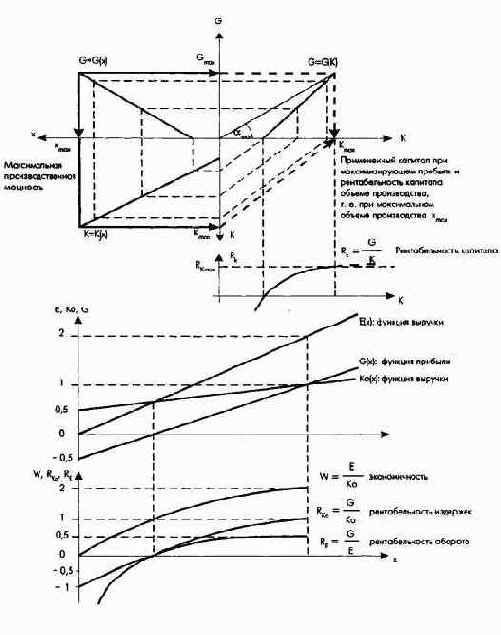
Рис. 30. Взаимосвязи между максимизацией прибыли, с одной стороны, и максимизацией рентабельности капитала, оборота, издержек и экономичности, с другой стороны
Наконец, следует учесть еще случай, когда функции издержек и выручки нелинейны. В этом случае максимизирующий прибыль объем производства меньше объема производства, максимизирующего выручку, что приводит к частично переменным связям между целями.
Таким образом, только при неизменности издержек или при линейных функциях издержек и выручки цели максимизации прибыли и оборота полностью взаимодополняют одна другую. В иных случаях взаимосвязи между целями частично непостоянны.
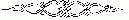
Линии "равной рентабельности" (изокривые рентабельности) - это геометрическое место точек, в которых произведение рентабельности оборота и скорости оборота капитала постоянно.
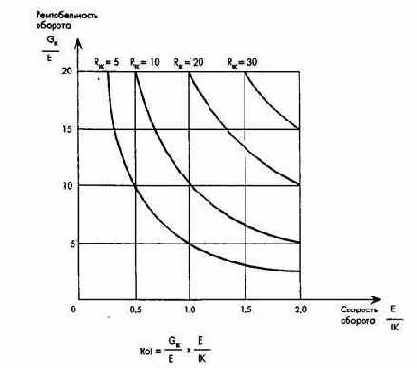
Рис. 27. Связи между рентабельностью капитала, рентабельностью оборота и скоростью оборота капитала
Определенный процент на инвестированный капитал, или определенная желаемая норма рентабельности капитала, может быть достигнут при различной величине рентабельности оборота. Кривые показывают, что, например, при скорости оборота капитала, равной 2, и рентабельности оборота 10% достигается такая же рентабельность капитала, как при оборачиваемости капитала, равной 1, и рентабельности оборота 20%.
Однако предположение о постоянстве капитала (собственного и заемного) в долгосрочной перспективе нереалистично.
При условии переменности (изменяемости) капитала максимум рентабельности капитала совпадает с максимумом прибыли только тогда, когда выполнено условие:
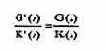
или когда эластичность прибыли равна эластичности капитала. Утверждение, что максимум прибыли не совпадает с максимумом рентабельности капитала, равноценно утверждению о том, что между целями максимизации прибыли и максимизации рентабельности капитала существуют локальные частично дополняемые и частично конкурирующие взаимосвязи целей.
Рассмотрим фундаментальный принцип формулирования целей, вытекающий из максимизации частного (правила частного). Для максимизации частного Q справедливо следующее:
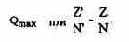
т.е. частное тогда достигает максимума, когда эластичность числителя равна эластичности знаменателя. Экономическое значение этого принципа для максимизации абсолютных и относительных целевых показателей огромно. Согласно нему просто объясняются связи между прибылью и показателями рентабельности даже тогда, когда частное содержит только показатели, из которых складывается прибыль, например только оборот и издержки, так что влияние чисто формальных различий в формулировке целей в разных предпринимательских решениях становится очевидным.
Перечисленные ниже относительные показатели можно максимизировать следующим образом:
рентабельность оборота
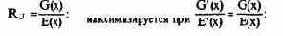
рентабельность издержек
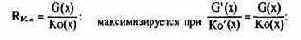
экономичность
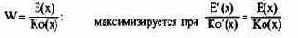
Преобразуя абсолютные величины в относительные, легко увидеть, что реализуется один и тот же принцип: эластичность числителя равна эластичности знаменателя. Если заменить в условии равновесия G на Е - К0, a G' на Е' - К0', то для трех величин получим одинаковые максимальные значения:
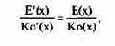
т.е. все три целевые величины будут максимизированы при одинаковом объеме производства х. Таким образом, несмотря на различное формулирование целей, на принятие предпринимательского решения оказывается одинаковое влияние. Вообще различие этих формулировок целей для максимизации прибыли очевидно, поскольку максимальное значение получается при
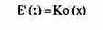
Между целями максимизации рентабельности оборота, рентабельности издержек и экономичности, с одной стороны, и целью максимизации прибыли, с другой стороны, существуют отношения как взаимодополнения, так и конкуренции целей. Из приведенных условий равновеси (уравнений максимизации) видно, что при максимизации прибыли встречаются только относительные (производные) показатели, а именно только Е'(х) и Ко'(х), при максимизации рентабельности в широком смысле - еще и абсолютные показатели, а именно G(x), К(х), Е(х) и Ко(х). Отсюда вытекает, что конкретные утверждения о соотношениях целей, областях дополнительных и конкурентных отношений между ними можно делать, если исходить из абсолютных величин издержек, выручки и капитала. Эти взаимосвязи можно показать графически, что обеспечивает достаточную точность.
3.1.2. Взаимосвязи между целевыми показателями прибыли и рентабельности при нелинейной функции прибыли
Прежде всего необходимо уточнить, каковы различия между максимизацией прибыли и максимизацией рентабельности капитала и тем самым связи между этими целевыми показателями. На рис. 28 во втором квадранте представлена функция прибыли G = G(x). При этом исходят из ее нелинейности, т.е. максимум прибыли достигается при объеме производства х = ОА.

Рис. 28. Связь между максимизацией прибыли и максимизацией рентабельности капитала
В третьем квадранте представлена линейная функция капитала К = К(х). Если спроецировать функцию прибыли на функцию капитала, то в первом квадранте получим функцию прибыли от инвестированного капитала, т.е. G = G(K). Проекцию можно объяснить на примере грех точек, через которые проходят штриховые линии проекции. Отрезки между точками этой кривой и осью абсцис образуют угол а. Тангенс угла а выражает рентабельность R = О/К. Рентабельность достигает максимума в точке, где отрезок линейной функции становится касательной кривой ОТ. Для получения этой максимальной рентабельности необходимо инвестировать капитал в размере OR, а для получения максимума прибыли - в размере OS. Максимизирующему рентабельность объему инвестируемого капитала OR соответствует максимизирующий рентабельность объем производства 0В, максимизирующий же прибыль объем производства равен ОА, но ОА^ОВ. Относительно объема производства х цели максимизации прибыли и максимизации рентабельности капитала в области 0В взаимодополняемы, а в области ВА - наоборот, конкурирующие. Прирост прибыли вызывает снижение рентабельности капитала. Относительно инвестируемого капитала К цели в области OR взаимодополняемы, а в области RS - конкурирующие.
После выявления взаимосвязей между максимизацией прибыли и максимизацией рентабельности капитала можно выявить взаимосвязи между максимизацией прибыли и максимизацией рентабельности оборота, рентабельности издержек и экономичности.
На рис. 29 изображены кривые издержек и выручки для двух важных случаев. В первом случае представлены кривая выручки при предполагаемой функции цена - сбыт и линейна функция издержек. Во втором случае представлена линейная функция выручки в условиях атомистической конкуренции и депрессивно-прогрессивная функция издержек. Из разности обеих функций получают функцию прибыли G = G(x). Далее на рисунке представлены кривые средних издержек (удельных, или штучных издержек), предельных издержек и предельной выручки.
Максимум прибыли получается в точке касания кривой прибыли и линии параллельной оси абсцис. Максимум прибыли в обоих, случаях равен Gmax = ОН. Максимизирующий прибыль объем производства в обоих случаях равен х = OF. При таком объеме производства кривая предельной выручки пересекает кривую предельных издержек в точке G. Касательная в точке Е показывает одинаковый подъем кривых выручки и издержек.
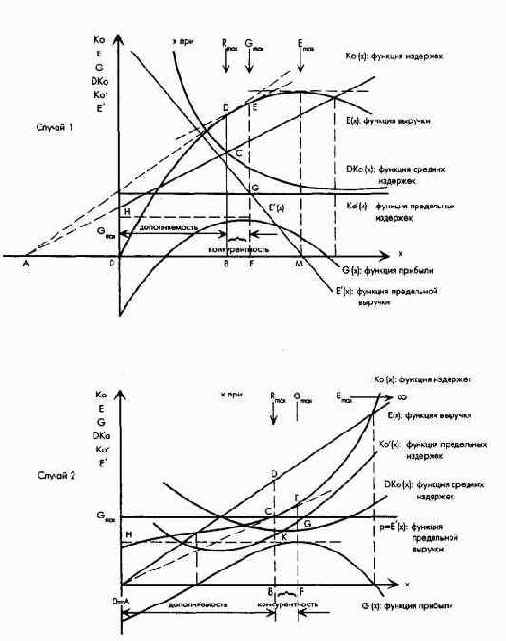
Рис. 29. Связи между максимизацией прибыли, с одной стороны, и максимизацией рентабельности оборота, рентабельности издержек и экономичности, с другой стороны (первый случай: заданы предполагаемая функция цена - сбыт и линейная функция издержек; второй случай: заданы условия атомистической конкуренции и дегрессивно-прогрессивная функция издержек)
Для определения объема производства, максимизирующего рентабельность оборота, действует условие:
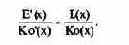
Поскольку
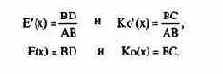
то отсюда следует:
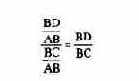
или
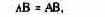
т.е. максимальная рентабельность оборота достигается при j АВ. Этот случай показан на рис. 29, где 0В является максимизирующим рентапбельность объемом производства. При этом
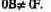
Таким образом, область от точки 0 до точки В является областью взаимодополнения целей, а от точки В до точки F - областью конкуренции целей. Увеличение объема производства сверх значения в точке В ведет к росту прибыли, но одновременно уменьшает рентабельность оборота, рентабельность издержек и экономичность. Во втором случае, представленном на рис. 29, максимизирующий рентабельность объем производства совпадает с производственным оптимумом, под которым понимается минимум средних издержек. В первом случае он не задан, поэтому производственный оптимум предприятия лежит в области бесконечности.
Оба случая совместны, поскольку одна из двух функций Е(х) или Ко(х) линейна. Здесь особенно легко применим метод касательных, ибо касательные к кривым линейных функций сами описываются линейными функциями. Необходимо только продолжить кривую до пересечения с осью абсцис. Эти соотношения не выдерживаются в случае, когда обе функции нелинейны.
3.1.3. Взаимосвязи между целевыми показателями прибыли и рентабельности при линейной функции прибыли
На рис. 30 эти взаимосвязи показаны для случая линейности всех функций.
Если исходить из линейных функций издержек и выручки, то получается уже не кривая прибыли с одним максимумом, а линейно возрастающая функция прибыли. Поскольку при исследовании взаимосвязей между целями максимизации прибыли и рентабельности капитала (рис. 28) исходили из того, что прибыль характеризуется кривой, и в рассматриваемом случае положим в основу также линейную функцию прибыли (рис. 30, верхняя часть). Очевидно, что максимум всех этих целевых показателей находится в области бесконечности. Если, однако, исходить из того, что при максимизации производственных средств предприятия объем производства будет максимальным и равным пределу производственной мощности (хmax), а выручка, соответствующая такому максимальному объему производства, будет максимальной, то и все целевые показатели также будут иметь свой максимум.
В случае линейного изменения издержек и выручки и роста функции издержек в меньшей степени, чем функции выручки, можно сформулировать принципиальное и исключительно важное для взаимосвязи целевых показателей следствие: все целевые показатели при условии линейности функций полностью взаимодополняемы, или, иначе, максимизирующий прибыль объем производства также максимизирует и рентабельность капитала, рентабельность издержек и экономичность. Этот объем производства является предельным относительно производственной мощности.
Для руководства предприятия отсюда вытекает простое, но важное правило: производить как можно больше, до тех пор, пока прибыль (или какой-либо из показателей рентабельности) не достигнет своего максимума. Поэтому, принимая предпринимательское решение, можно руководствоваться любыми из вышеназванных целевых показателей, поскольку в данном случае выбор различных целей влечет за собой одинаковые последствия.